在数据分析的旅程中,发现并理解数据之间的差异是解锁关键洞察的核心。无论你是研究不同群体的特征,还是评估策略的效果,差异分析都是不可或缺的工具。本文将带你快速了解差异分析的基本流程、常用方法及实际应用,帮助你掌握如何从数据中发现有价值的差异,为你的研究或决策提供有力支持。
1. 数据探索:
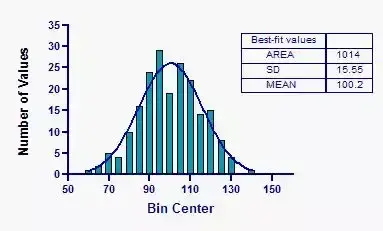
绘制概率数据的直方图或箱线图,观察数据是否呈现“中间高,两头低”的钟形分布
2. 正态性和方差齐性检验:
根据数据的正态性及方差齐性来判断使用什么统计分析方法。不符合正态分布或不满足方差齐性的数据可以进行数据转换,或直接采用非参数方法进行分析。
Graphpad实操
- 正态性检验:
- 单个参数数据导入 Column 类型表格中;
- 点击 Analyze,选择 Column analyses;
- 选择 Normality and Lognormality Tests,对每组数据进行正态性检验;
- 如果数据符合正态分布(P > 0.05),则可以继续进行分析。
- 常用简易方法:
-
点击 Analyze,根据分组数量选择 t-tests 或者 One-way ANOVA;
-
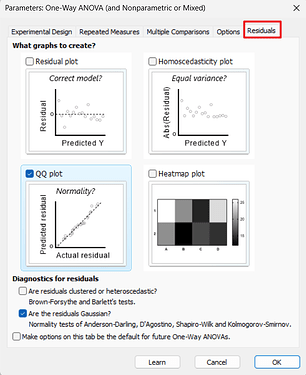
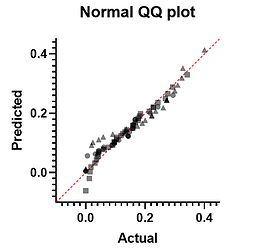
Experimental Design 标签页中先均假设数据符合正态性与方差齐性,Residuals 标签页中勾选 QQ plot 和 Are the residuals Gaussian?;
-
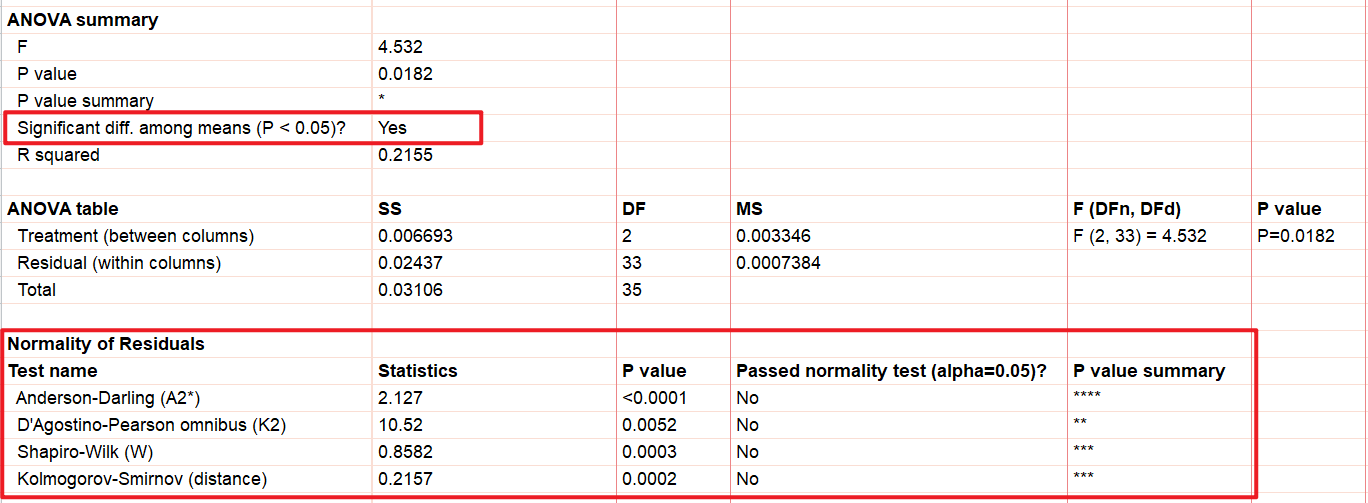
查看结果页中的 Are SDs significantly different (P<0.05)? 和 Normality of Residuals 的结果,根据Yes和No判断数据情况;
-
如果数据不符合正态分布或方差不齐性,则在 Analyzer 中勾选对应的数据情况,采用合适的分析方法;
-
如果数据符合正态分布(P > 0.05),且方差齐性,则该差异分析结果有意义,或者可以将多参数数据合并进行Two-way ANOVA分析;
-
Graphpad中正态性检验有多种方法,不同方法的特点分别为:
- Shapiro-Wilk检验:适用于小样本(n < 50),对数据的正态性检验较为敏感。
- D’Agostino-Pearson检验:综合考虑偏度和峰度,适用于中等样本量,是GraphPad Prism推荐的检验方法。
- Kolmogorov-Smirnov检验:不推荐使用,因为它对样本量较小的情况不够敏感
当不同检验方法的结果不一致时,根据数据情况选取适合的方法解读数据情况。
正态性检验最好结合直方图(是否钟形分布)或Q-Q图(是否线性分布)判断,特别是当样本量少于10或多于100时,结果以图为准。
3. 数据转换:
当数据不符合正态分布时,数据转换是一种常用的方法,可以帮助改善数据的正态性和方差齐性,从而满足统计分析的假设条件。以下是一些常用的非正态数据转换方法:
1. 对数转换(Log Transformation)
- 公式:
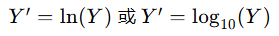
- 适用场景:适用于数据呈右偏分布(即大部分数据集中在较小的值,少数数据为较大的值)。对数转换可以压缩大值,拉伸小值,使数据更接近正态分布。
- 注意事项:数据必须为正值。如果数据中包含0或负值,需要先进行平滑处理,例如将所有数据加上一个小常数(如1)。
2. 平方根转换(Square Root Transformation)
- 公式:
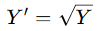
- 适用场景:适用于数据呈右偏分布,尤其是计数数据(如泊松分布)。平方根转换可以减少数据的变异性,使数据更接近正态分布。
- 注意事项:数据必须为非负值。如果数据中包含负值,需要先进行平滑处理。
3. 倒数转换(Reciprocal Transformation)
- 公式:
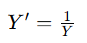
- 适用场景:适用于数据呈右偏分布,尤其是当数据的范围较宽时。倒数转换可以将大值转换为小值,小值转换为大值,从而改善数据的分布。
- 注意事项:数据必须为非零值。如果数据中包含0,需要先进行平滑处理,例如将所有数据加上一个小常数(如1)。
4. Box-Cox转换(Box-Cox Transformation)
- 公式:
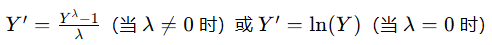
- 适用场景:Box-Cox转换是一种参数化的转换方法,可以找到最适合数据的转换参数 λ。适用于各种类型的非正态数据。
- 注意事项:数据必须为正值。如果数据中包含0或负值,需要先进行平滑处理。
5. 反正弦转换(Arcsine Transformation)
- 公式:
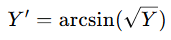
- 适用场景:适用于比例数据(如百分比数据),尤其是当数据范围在0到1之间时。反正弦转换可以改善比例数据的正态性和方差齐性。
- 注意事项:数据必须在0到1之间。如果数据超出这个范围,需要先进行归一化处理。
6. 对数几率转换(Logit Transformation)
- 公式:
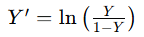
- 适用场景:适用于比例数据(如概率值),尤其是当数据范围在0到1之间时。对数几率转换可以将概率值映射到整个实数范围,改善数据的正态性和方差齐性。
- 注意事项:数据必须在0到1之间,且不能包含0或1。如果数据中包含0或1,需要先进行平滑处理,例如将0替换为一个非常小的正数(如 1×10−6),将1替换为一个非常接近1的数(如 1−1×10−6)。
7. Probit转换(Probit Transformation)
- 公式:

- 适用场景:适用于比例数据(如概率值),尤其是当数据范围在0到1之间时。Probit转换可以将概率值映射到整个实数范围,改善数据的正态性和方差齐性。
- 注意事项:数据必须在0到1之间,且不能包含0或1。如果数据中包含0或1,需要先进行平滑处理。
选择合适的数据转换方法
选择哪种数据转换方法取决于数据的分布特性。以下是一些选择建议:
- 如果数据呈右偏分布,可以尝试对数转换或平方根转换。
- 如果数据是比例数据(如概率值),可以尝试反正弦转换、对数几率转换或Probit转换。
- 如果数据范围较宽,可以尝试倒数转换。
- 如果不确定哪种转换最适合,可以尝试多种转换方法,然后通过正态性检验(如Shapiro-Wilk检验)和方差齐性检验(如Levene检验)来评估转换效果。
- 在一些方法中无法对0或1值进行转换,因此需要手动对数据进行平滑处理,将0值替换为一个非常小的正数,将1值替换为一个非常接近1的数。
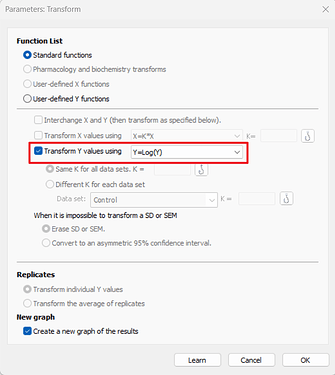
Graphpad实操:
- 点击菜单栏中的 Analyze;
- 选择 Transform, Normalize…,然后选择 Transform;
- 选择合适的转换公式;
- 对转换后的数据重新进行正态性和方差齐性检验,确认是否满足假设条件。
4. 选择合适的分析方法:
如果转换后的数据满足假设条件,可以使用ANOVA;否则,考虑非参数方法或混合效应模型。
所有参数的Two-way ANOVA vs. 单个参数的One-way ANOVA
Two-way ANOVA
- 优势
- 考虑交互作用:可以同时分析两个因素(实验组和嗅闻动作类别)对挖掘动作转移概率的影响,以及这两个因素之间是否存在交互作用。例如,可以判断不同实验组中,某种嗅闻动作对挖掘动作转移概率的影响是否因实验组的不同而有所差异。
- 更全面的分析:能够更全面地了解数据中不同因素的综合影响,有助于揭示潜在的复杂关系。
- 劣势
- 数据要求更高:需要更多的数据来满足统计检验的假设条件,如独立性、正态性和方差齐性等。如果数据量不足或不符合这些假设,可能会导致分析结果的可靠性降低。
- 复杂度增加:分析过程相对复杂,需要考虑更多的因素组合和交互效应,对数据的理解和解释要求更高。
One-way ANOVA
- 优势
- 简单易行:分析过程相对简单,计算量较小,对数据的要求相对宽松。适合在数据量有限或对交互作用不感兴趣的情况下使用。
- 针对性强:可以单独分析每种嗅闻动作对挖掘动作转移概率的影响,结果更直接、更易于解释。
- 劣势
- 忽略交互作用:无法考虑实验组和嗅闻动作类别之间的交互作用。如果这种交互作用实际上存在且对结果有重要影响,那么使用One-way ANOVA可能会遗漏一些重要的信息。
- 分析不够全面:只能分析单一因素的影响,无法同时考虑多个因素的综合影响。
其他方法推荐
- 混合效应模型(Mixed-effects Model):如果实验设计中存在嵌套结构或重复测量的情况,混合效应模型可能是一个更好的选择。它可以同时考虑固定效应(如实验组和嗅闻动作类别)和随机效应(如个体间的差异),从而更准确地估计各因素对挖掘动作转移概率的影响。
- 多元线性回归(Multiple Linear Regression):当需要同时考虑多个自变量(如实验组、嗅闻动作类别以及其他可能的协变量)对因变量(挖掘动作转移概率)的影响时,多元线性回归是一个有效的工具。它可以提供更灵活的模型拟合和更详细的参数估计。
- 重复测量方差分析(Repeated Measures ANOVA):如果在实验中对同一组小鼠进行了多次测量(例如,在不同时间点或不同条件下观察其嗅闻和挖掘行为),重复测量方差分析可以考虑这种重复测量的结构,从而更准确地分析数据。
综上所述,选择哪种方法取决于你的具体研究问题、数据结构以及你对交互作用的兴趣。如果需要同时考虑实验组之间的差异,并且对参数之间的交互作用感兴趣,那么Two-way ANOVA是一个合适的选择。如果更关注每个参数的单独影响,且对交互作用不感兴趣,那么可以考虑使用One-way ANOVA。同时,也可以根据数据的特点和研究需求,考虑使用混合效应模型、多元线性回归或重复测量方差分析等其他方法。